CS 330: Lecture 36 – Taming Recursion
Dear students,
We’ve seen that Haskell does some pretty crazy things: it infers types, it supports this crazy pattern matching stuff, it disallows side effects, and it computes things lazily. Let’s look at one last crazy thing it does: it uses recursion for everything! There are no loop control structures.
Normally, when you think of recursion, what’s the first thing that comes to mind?
Performance is probably not what you’re thinking of. I think stack overflow exceptions. Why does recursion lead to stack overflow exceptions? Because every time you call a function, we throw onto the stack a new stack frame holding the function’s parameters, local variables, and
Today we’re going to look at two tricks that can make recursive algorithms have much better performance.
The first of these is called memoization. We define it as follows:
Memoization is the act of caching the result of a routine to speed up subsequent invocations of that routine.
We’ve already seen memoizing once. When we added lazy evaluation to Ruby using our Lazy class, we delayed the computation by putting it in a block, and then cached its result the first time it was executed. Today we’re going to use a similar idea to make repeated recursive function calls really speedy.
Let’s start off by visualizing a recursive algorithm. I really have no tolerance for several tired old programming problems: the Towers of Hanoi, Fahrenheit to Celsius conversion, the shape hierarchy, and the Fibonacci sequence. However, the familiarity of these problems is actually helpful today. Let’s look at a Fibonacci “tree” for the sixth Fibonacci number:

What do you notice? What happens when we compute the seventh Fibonacci number?
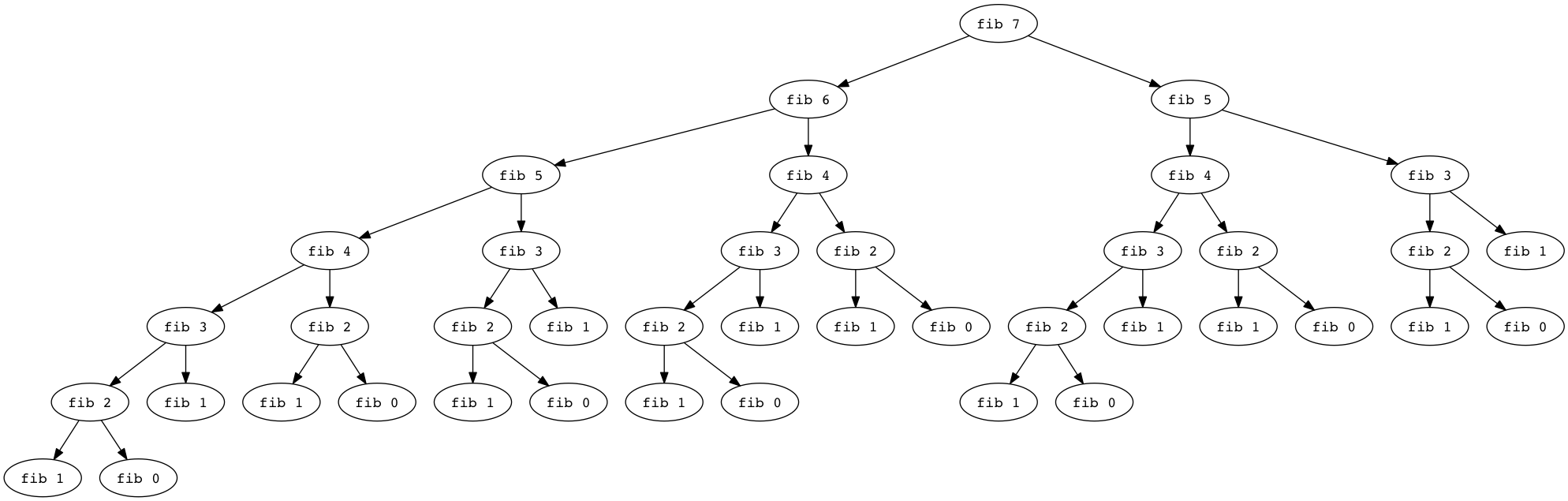
That’s a lot of duplicated calls, eh? Is that a big deal? Maybe not. Let’s try implementing it:
def fib n
if n <= 1
n
else
fib(n - 1) + fib(n - 2)
end
end
n = ARGV[0].to_i
puts fib n
Let’s see how well this scales. We’ll try various values of n and see what happens.
We’ll find that all this duplication does indeed takes its toll. What if somehow we could cache the value of a “tree” and not have to recurse through it if we’d already done so? Let’s try. But how will we do this? How do we remember what the results are for a previous tree? Well, we can create a dictionary mapping the function’s parameter to its return value. Like this:
$cache = Hash.new
def fib n
if $cache.has_key? n
$cache[n]
else
value = fib(n - 1) + fib(n - 2)
$cache[n] = value
end
end
n = ARGV[0].to_i
puts fib n
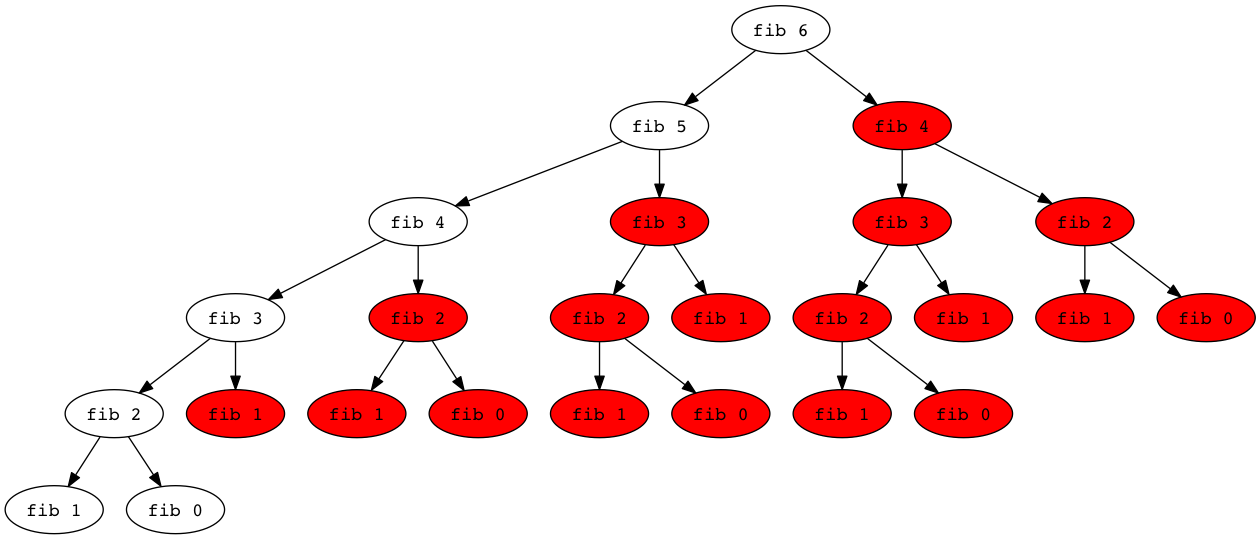
This is a whole lot faster. How much work have we saved? Well, look at this tree for fib 6:
And for fib 7:
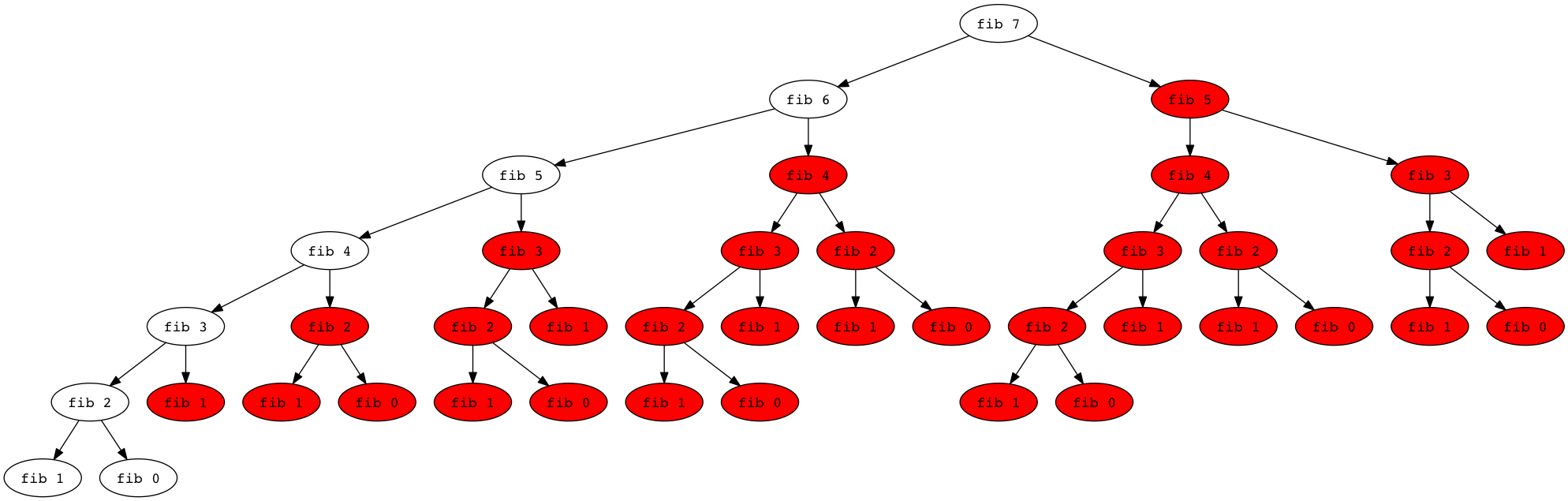
We have turned what was an algorithm of exponential complexity into one of linear complexity—assuming the cost of dictionary lookup is neglible.
That’s great, but having to explicitly add memoization to the function is kind of annoying. What we added had very little to do with the Fibonacci sequence. Hmm… Maybe we could write a higher-order function that automatically wrapped up a function inside a memoizing routine? Yes, we can. In fact, the technique we’ll use is called method wrapping. And we can also get rid of that nasty global cache.
It would be great if we could write something like this:
fib = memoize(fib)
That way we could continue to call fib like normal. Memoization would just be an implementation detail, as it should be.
Let’s solve this in steps. The memoizing function will need to accept another function as its parameter. We’re going to use Ruby symbols for this, which are kind of like method references in Java 8:
def memoize fid
...
end
fib = memoize(:fib)
Also, the arity of functions is going to be important here. For the time being, let’s say our function only works with functions of arity 1:
def memoize1 fid
...
end
fib = memoize1(:fib)
Next, we’ll need a cache:
def memoize1 fid
cache = Hash.new
...
end
Then let’s overwrite our function with a new one. We’ll use some Ruby magic for this:
def memoize1 fid
cache = Hash.new
define_method(fid) do |arg|
# method body here
end
end
Hang on. If we overwrite our function with this memoizing wrapper, we won’t be able to call the real one when we need it. Let’s retain a reference to the old one. Here’s a complete wrapper which adds absolutely no extra work around the function:
def memoize1 fid
cache = Hash.new
f = method(fid)
define_method(fid) do |arg|
f.call arg
end
end
Let’s add the memoization work:
def memoize1 fid
f = method(fid)
cache = Hash.new
define_method(fid) do |arg|
if cache.has_key? arg
cache[arg]
else
value = f.call arg
cache[arg] = value
end
end
end
Closures to the rescue here! They saved us from our global cache. First-class functions to the rescue too! We stored the old function in a local variable that is also referenced by the closure.
For the curious, we can also generalize this code to work for functions of arbitrary arity using Ruby’s splat operator:
def memoize fid
f = method(fid)
cache = Hash.new
define_method(fid) do |*args|
if cache.has_key? args
cache[args]
else
value = f.call *args
cache[args] = value
end
end
end
Let’s try this out on a different recursive function, for a problem taken from the MICS 2017 programming contest. Suppose you are standing at an intersection of a city. You are trying to get to a certain other intersection. How many ways can you get there, assuming you never go out of your way?
Consider this example where you are 3 blocks north and 2 blocks west of your destination. You could go DDRRR, DRDRR, DRRDR, DRRRD. Or RRDRD, RRRDD, RDDRR, RDRDR, RDRRD, or RRDDR. That’s ten different options.
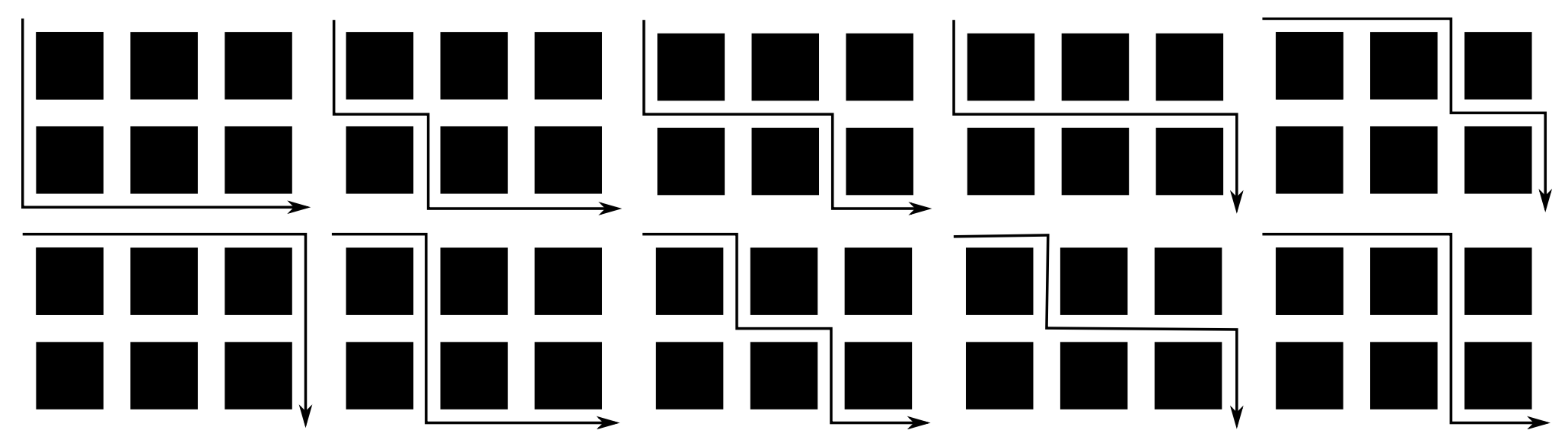
Like most recursive problems, this feels really obtuse but has a simple solution:
def nroutes x, y
if x == 0 && y == 0 # We've arrived!
1
elsif x < 0 || y < 0 # We're gone out of our way. Illegal.
0
else
nroutes(x - 1, y) + # How many paths if we right?
nroutes(x, y - 1) # How many paths if we down?
end
end
When we run this, it start to get bogged down very quickly. But there’s a lot of tree revisiting here, just as with Fibonacci. Let’s memoize:
memoize(:nroutes)
And it’s beautifully fast.

P.S. It’s time for a haiku!
Teachers may seem smart
But before they’ve memoized
They’re pretty much you
P.P.S. Here’s the code we wrote together:
fib.rb
#!/usr/bin/env ruby
$cache = Hash.new
def fib(n)
if !$cache.has_key?(n)
if n < 2
$cache[n] = 1
else
$cache[n] = fib(n - 2) + fib(n - 1)
end
end
$cache[n]
end
def memoize1(fid)
cache = Hash.new
f = method(fid)
define_method(fid) do |arg|
if !cache.has_key?(arg)
cache[arg] = f.call(arg)
end
cache[arg]
end
end
def memoize2(fid)
cache = Hash.new
f = method(fid)
define_method(fid) do |arg1, arg2|
args = [arg1, arg2]
if !cache.has_key?(args)
cache[args] = f.call(arg1, arg2)
end
cache[args]
end
end
def fib2(n)
if n < 2
1
else
fib(n - 2) + fib(n - 1)
end
end
fib2 = memoize1(:fib2)
# puts fib2(10)
# puts fib2(100)
def nroutes(x, y)
if x == 0 && y == 0
1
elsif x < 0 || y < 0
0
else
nroutes(x - 1, y) + nroutes(x, y - 1)
end
end
nroutes = memoize2(:nroutes)
puts nroutes(130, 70)