CS 330 Lecture 13 – Vtables and Graphing Calculator
Dear students,
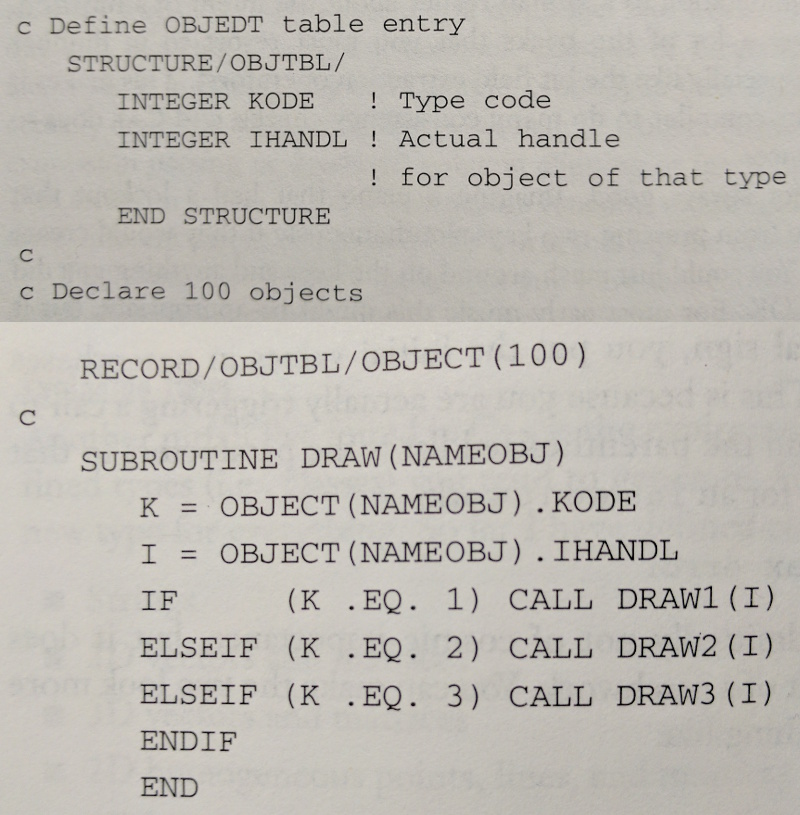
We saw last time that for subtype polymorphism to work in languages like Java and C++, we need some for way for each object to carry around some information to help us figure out what method to call at runtime. What exactly is that information and how does the runtime decision—the dynamic dispatch—get made? Computer graphics pioneer Jim Blinn wrote a column in 1990s when C++ was gaining in popularity, and he dismissed polymorphism, saying he’d doing something like that in Fortran for the longest time. Here’s his polymorphism in Fortran:
Subroutine DRAW is the conductor code. It walks through a conditional ladder, inspects a type tag, and dispatches accordingly. This looks a lot like our dynamic typing system we wrote in C.
If this was how dynamic dispatch was implemented, its designer would have been eaten alive on Reddit and Stack Overflow. Why? For one, the conductor code is full of conditional statements. We saw in computer architecture that conditional statements thwart pipelining. For two, every time we add a new type to our hierarchy, we have to go back to the conductor code and update it. We’d really like to avoid touching code once it’s working. We tend to mess stuff up. There’s that saying, “separate that which changes from that which doesn’t.” This is why we make battery compartments. This is why we use domain names instead of IP addresses. This is why oil filters are always in locations that are easy to access. jk
Thankfully, dynamic dispatch is implemented differently.
Each class with virtual methods gets a special spot in memory called a vtable, or virtual table. This table is stored per class, not per instance. It’s static.
Let’s examine a class hierarchy (courtesy of Stroustrup) and see how these virtual tables are laid out:
class A { public: virtual void f(); virtual void g(int); virtual void h(double); void i(); int a; }; class B : public A { public: void g(int); virtual void m(B*); int b; }; class C : public B { public: void h(double); virtual void n(C*); int c; }
The vtable of A looks like this:
| Function | Address |
|---|---|
| f | &A::f |
| g | &A::g |
| h | &A::h |
Method i gets no entry, because it is not virtual.
The vtable of B looks like this:
| Function | Address |
|---|---|
| f | &A::f |
| g | &B::g |
| h | &A::h |
| m | &B::m |
Class B overrides g and adds m. Its other entries just point to A‘s code.
The vtable of C looks like this:
| Function | Address |
|---|---|
| f | &A::f |
| g | &B::g |
| h | &C::h |
| m | &B::m |
| n | &C::n |
These vtables are stored once per class—they’re static. Each instance of A, B, or C has an implicit instance variable pointing to its class’ vtable. We’ll call that member vptr. An instance of A is laid out like this in memory:
| a |
| vptr |
An instance of B is laid out like this in memory:
| a |
| vptr |
| b |
An instance of C is laid out like this in memory:
| a |
| vptr |
| b |
| c |
Now, suppose we have a piece of conductor code that takes in a pointer to A, but under the hood the object is an instance of C:
void conduct(A *p) { p->g(11); }
What exactly has to happen here to get the right code running?
- We must conjure up
p‘svptr. - In the table pointed to by
p->vptr, we must locate the address of the code forg. - We must call that code with both the invoking object and 11 as parameters.
Under the hood, this invocation turns into crazy indirect memory lookup. We get a function pointer from the vtable pointed to by the object and call it:
(*(*p->vptr)["g"])(p, 11);
So, subtype polymorphism is made fast at runtime through a table lookup. No conditionals are needed. Is this indirection free? No, because there are memory reads. Will these memory reads be fast? The vtables will likely be stored in cache if they are frequently accessed. They are small and there’s only one per class. The object is also likely to be in cache if we’re operating on it.
Now let’s put subtype polymorphism to work in a Curses-based graphic calculator. Let’s start with an abstract base class for all functions:
class Function { public: virtual double operator()(double x) const = 0; };
Now let’s recast our linear and quadratic functions as independent subtypes of Function:
class QuadraticFunction : public Function { public: QuadraticFunction(double a, double b, double c) : a(a), b(b), c(c) { } double operator()(double x) const { return a * x * x + b * x + c; } private: double a, b, c; }; class LinearFunction : public Function { public: LinearFunction(double a, double b) : a(a), b(b) { } double operator()(double x) const { return a * x + b; } private: double a, b; };
And now we create a graphic calculator class. It will be our conductor code, knowing only about Functions but not any particular subtype:
class Calculator { public: Calculator() { initscr(); clear(); getmaxyx(stdscr, height, width); } void add(Function *f) { functions.push_back(f); } void plot() { int mid_x = width / 2; int mid_y = height / 2; for (int x = 0; x < width; ++x) { mvprintw(mid_y, x, "."); } for (int y = 0; y < height; ++y) { mvprintw(y, mid_x, "."); } for (int x = -mid_x; x <= mid_x; ++x) { for (auto fp : functions) { const Function &f = *fp; int y = f(x); mvprintw(mid_y - y, x + mid_x, "o"); } } getch(); endwin(); } private: int width; int height; vector<Function *> functions; };
And finally, a main method to put it all together:
int main(int argc, char **argv) { QuadraticFunction f(0.1, 0, -15); Calculator calc; calc.add(&f); calc.plot(); return 0; }
True polymorphism lets us add new types to this system without modifying the conductor code. Let’s make a derivative class:
class FunctionDerivative : public Function { public: FunctionDerivative(const Function &f) : f(f) { } double operator()(double x) const { const double DELTA = 0.001; return (f(x + DELTA) - f(x - DELTA)) / (2 * DELTA); } private: const Function &f; };
A real derivative would examine the change in x as y gets infinitesimally small. Let’s pretend we’re happy with finite differencing. The FunctionDerivative class becomes a second conductor. It doesn’t know what sort of Function its computing the derivative for.
In our main, we can get the derivative plotted without modifying the calculator in any way (or shape or form!):
FunctionDerivative fprime(f); ... calc.add(&fprime);
Here’s your TODO list for next time:
- Read this interview with Bjarne Stroustrup, inventor of C++. Write down 2-3 questions or observations inspired by the article.
See you then!