CS 1: Lecture 17 – If Diversions
Dear students,
We now turn to another model of logic: Venn diagrams. In the late 1800s, logician John Venn invented a diagram for showing ideas of logic. He writes:
I began at once somewhat more steady work on the subjects and books which I should have to lecture on. I now first hit upon the diagrammatical device of representing propositions by inclusive and exclusive circles. Of course the device was not new then, but it was so obviously representative of the way in which any one, who approached the subject from the mathematical side, would attempt to visualise propositions, that it was forced upon me almost at once.
In a Venn diagram, each circle represents a subgroup of some larger universe. For instance, we might have circle A represent deciduous trees. Circle B might represent coniferous trees. These two groups do overlap. Maple, oak, and elm are purely deciduous. Pine and spruce are purely coniferous. Bald cypress, larch, and tamarack are both. A cactus is neither.
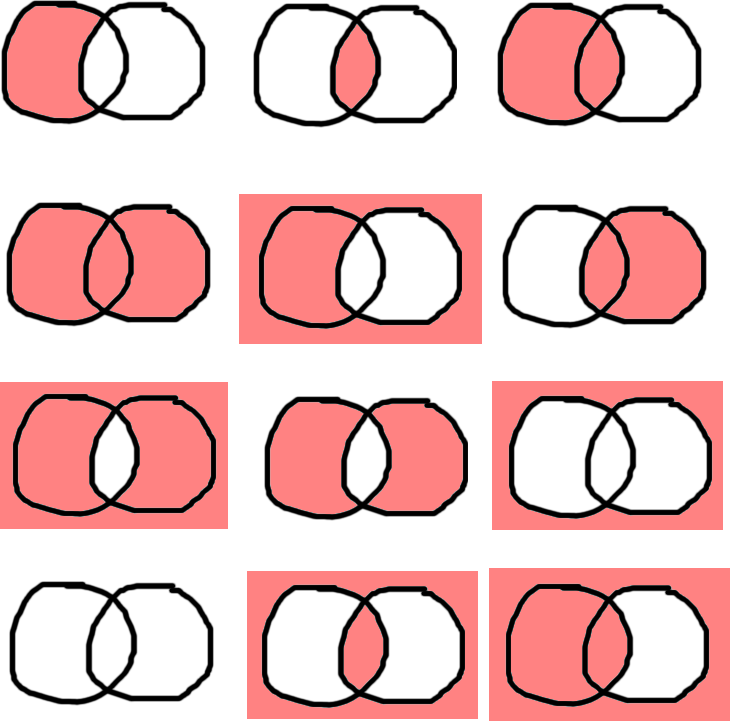
Let’s do another little exercise. I will show a series of Venn diagrams. Circle A is on the left, Circle B is on the right. Your task is to write boolean expressions that are true for the shaded area of each diagram. For example, the first diagram is a && !b.
Now, on to something else. We’ve seen the computer as a calculator, crunching numbers. We’ve seen the computer as a chef, calling upon recipes of code. We’ve seen the computer as a philosopher, considering truths about our data. Now it’s time to let those truths drive our computer’s actions. We will see the computer as a pilot, navigating wild routes through our code based on conditions.
Normally, the flow of control in a program goes from the top of a method to its bottom, one statement after another. The ball gets rolling in main, and it may temporarily pause its execution to let another method do some work. But in general, it’s one statement after another. But sometimes we want to do some extra work under certain conditions. I call this pattern a diversion, and we structure it like so:
// pre work
if (booleanCondition) {
// diversion work
}
// post work
The key observation here is that the diversion doesn’t always get executed. Only when booleanCondition is true. Let’s see this pattern in some real contexts:
- cat meowing in Scratch
- cat avoiding mouse in Scratch
absensureAddresspluralize
Next time we’ll visit choices where there are more than two options.
Here’s your TODO list to complete before we meet again:
- Read chapter 4 through section 4.1 in your book. On a quarter sheet, write an example
ifstatement that guides the actions of your life. Here’s one for me:Make sure the then-block contains statements or actions. Unlike a passiveif (fridge.contains(ORANGE_JUICE)) { drink(ORANGE_JUICE); hitPoints += 10; }
booleanexpression,ifstatements do something. - The homework 2 peer review session will take place in lab this week. To receive credit for the homework, you must attend. If you didn’t not receive credit, do not attend a peer review session.
- I am traveling to a conference this weekend to present some of my work. We will not formally meet Friday or Monday. However, I will be sending you a few videos to watch. Check your email.
See you next class!

P.S. It’s time for a haiku!
If it’s going up
Hop on; otherwise, hop on
Elevators are fun
P.P.S. Here’s the code we wrote together in class…
Diversions.java
package lecture1016;
public class Diversions {
public static void main(String[] args) {
System.out.println(abs(6));
System.out.println(ensureAddress("obrybry@uwec.edu"));
System.out.println(getQuantifiedMessage(0));
}
public static int abs(int x) {
if (x < 0) {
x = -1 * x; // this was their idea
x = -x;
x *= -1;
}
return x;
}
public static String ensureAddress(String address) {
if (!address.endsWith("@uwec.edu")) {
// address = address + "@uwec.edu";
address += "@uwec.edu";
}
return address;
}
public static String getQuantifiedMessage(int quantity) {
String s = "You've got " + quantity + " new message";
if (quantity != 1) {
s += "s";
}
return s + "!";
}
}