Another Integer Triangle Wave
I’ve across another way to generate a triangular wave. So exciting!
Recall from last time that I want to generate a pattern that looks like this:
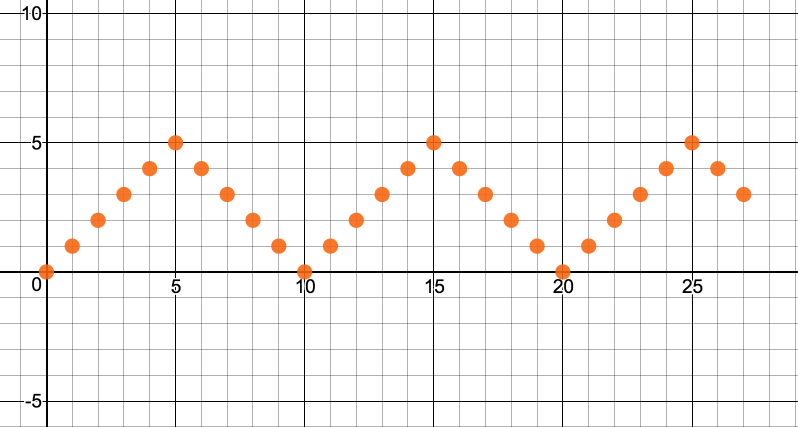
In this example, the period is 10.
As before, we can generate a sawtooth wave with some help from modulus:
$$y = \textrm{mod}(x, \textrm{period})$$
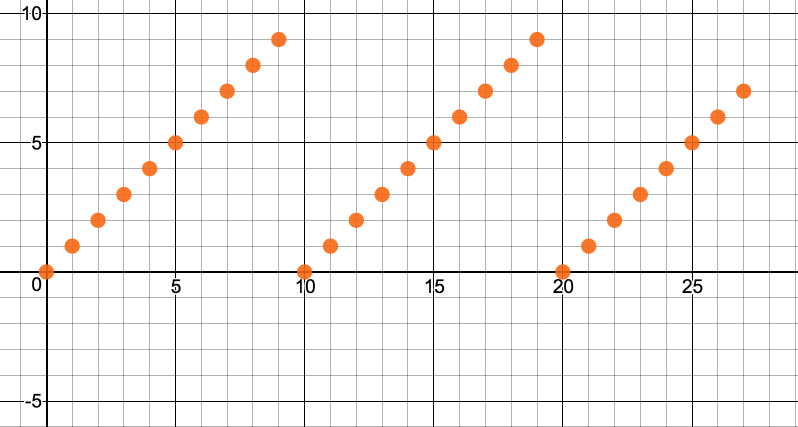
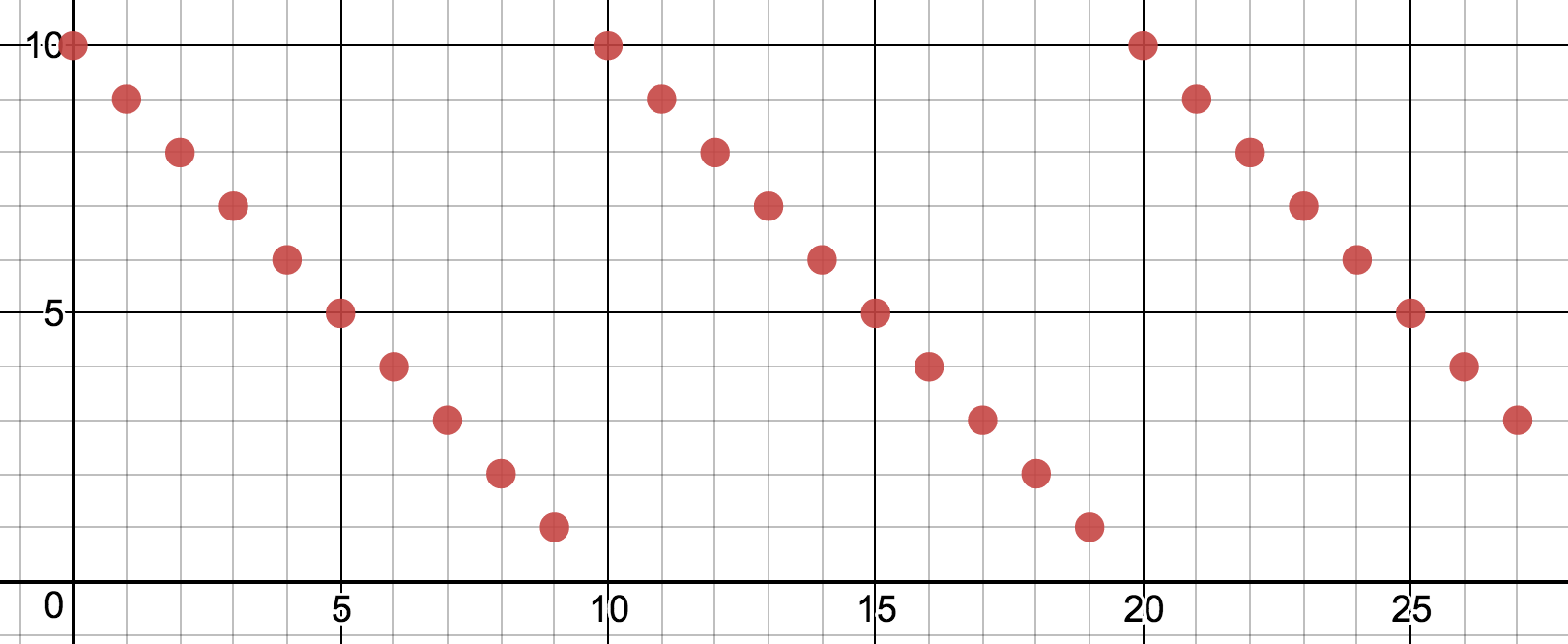
We can also generate a flipped sawtooth wave by taking the complement of the period:
$$y = \textrm{period} – \textrm{mod}(x, \textrm{period})$$
Let’s superimpose these real quick:
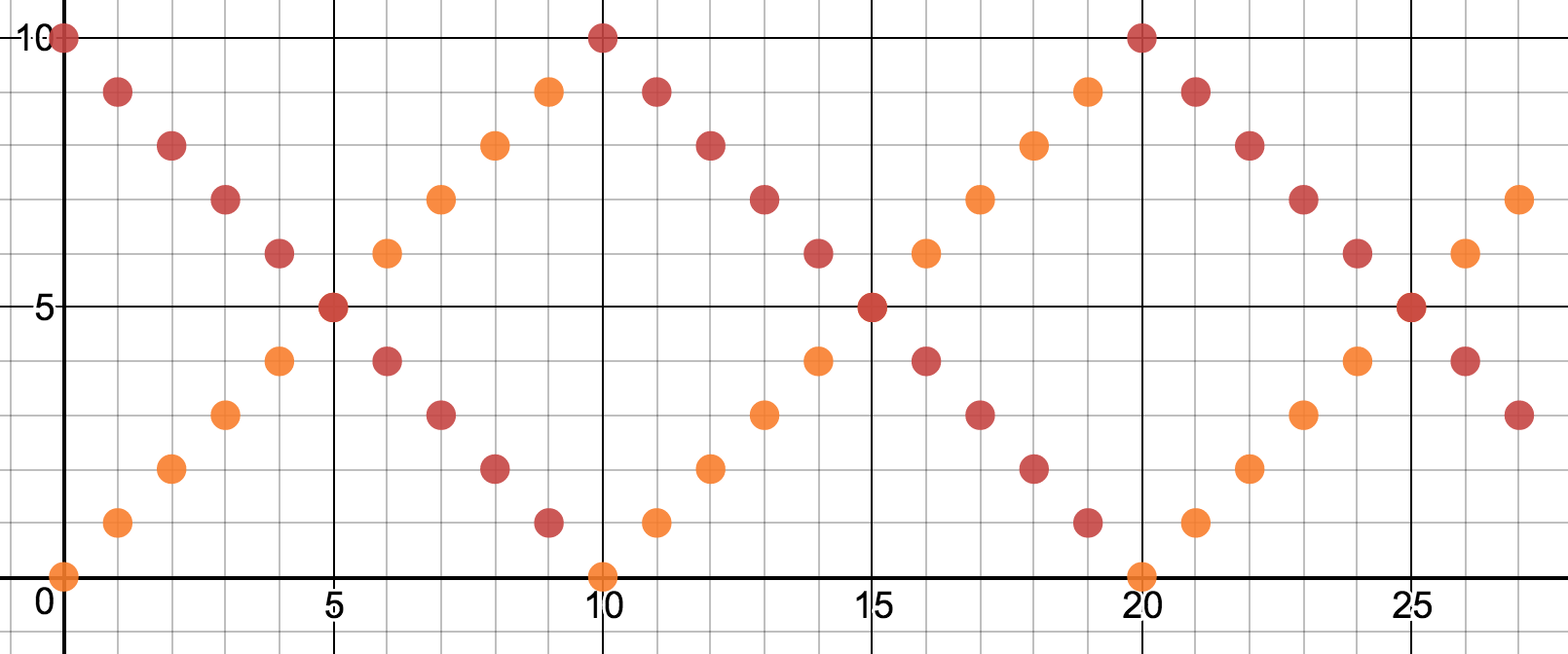
The wave I want is in there. It’s the bottom half of the weave. We can select out the bottom half with the min function:
$$y = \min(\textrm{mod}(x, \textrm{period}), \textrm{period} – \textrm{mod}(x, \textrm{period}))$$
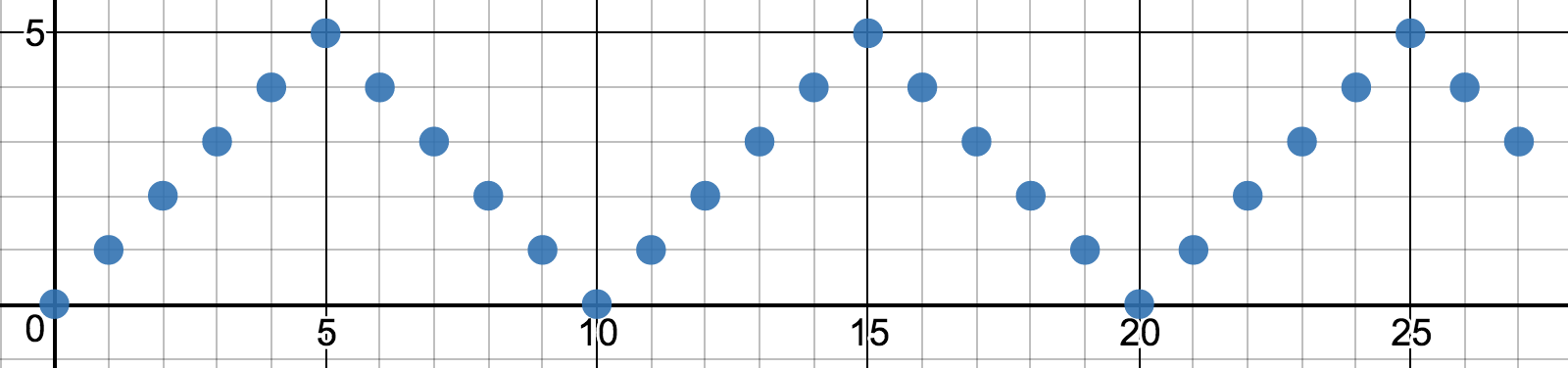
The graph I used to think this through is on Desmos.