The Tiangle, Part II
This post is part of a series of notes and exercises for a summer camp on making musical instruments with Arduino and Pure Data.
We have an Arduino setup that allows the player to crank a knob to produce numbers on the serial port. Now it’s time to add the music. In this exercise, we create a Pure Data patch that reads the single-byte readings and feeds them to an oscillator.
Pure Data Interpreter
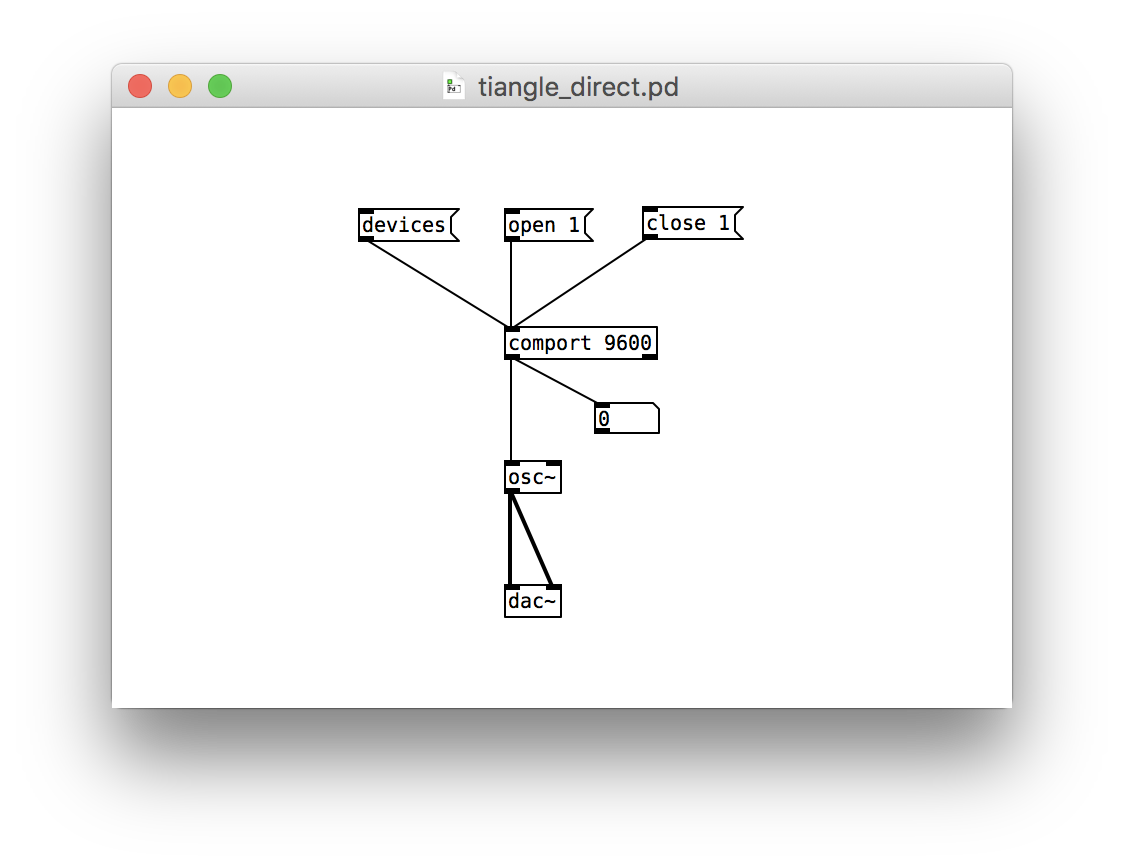
Here’s our first go at this patch:
The comport object is a bit like the Serial Monitor of the Arduino development environment. It reads data from the serial communications port. But instead of printing the numbers it reads, it sends them along through its outlet. The three boxes above comport and connected to its inlets are messages. When you click on the devices message, you get a list of devices connected to the serial port. open 1 connects to the first device in that list. close 1 disconnects from that device.
Let’s build it. First, unplug the Arduino from your computer and close the Serial Monitor. Only one program can read from the serial port at a time.
Then recreate this patch in Pure Data. Use Put / Message to add the messages.
Once you’ve got your patch, leave Edit Mode. Reconnect the Arduino, click devices, and find your Arduino. It may take a few seconds for the list to appear. If your Arduino is not device 1, change the parameters for the open and close messages accordingly. Hit open. Crank that potentiometer and let the sound fly!
Right? It probably doesn’t do what you want. The problem is that Serial.println in the Arduino sketch sends the reading not as a number, but as text. Instead of sending 207, for example, it sends characters 2, then 0, and then 7 all as separate bytes. Let’s fix this. First hit the close message to disconnect from the serial port. Then change Serial.println to Serial.write, which sends each reading as a single byte. Verify and upload the sketch, and then return to Pure Data. Hit open and see if it sounds better.
Fine Tuning the Frequencies
We now have physical control over the sound waves that are being produced. The only hitch is that a lot of the frequencies in [0, 255] are outside the range that we can hear, and 255 different frequencies is a pretty narrow range. Let’s modify the patch to emit a wider and more audible range of frequencies.
Right now, we’ve got this relationship between the potentiometer’s angle and the emitted frequency:
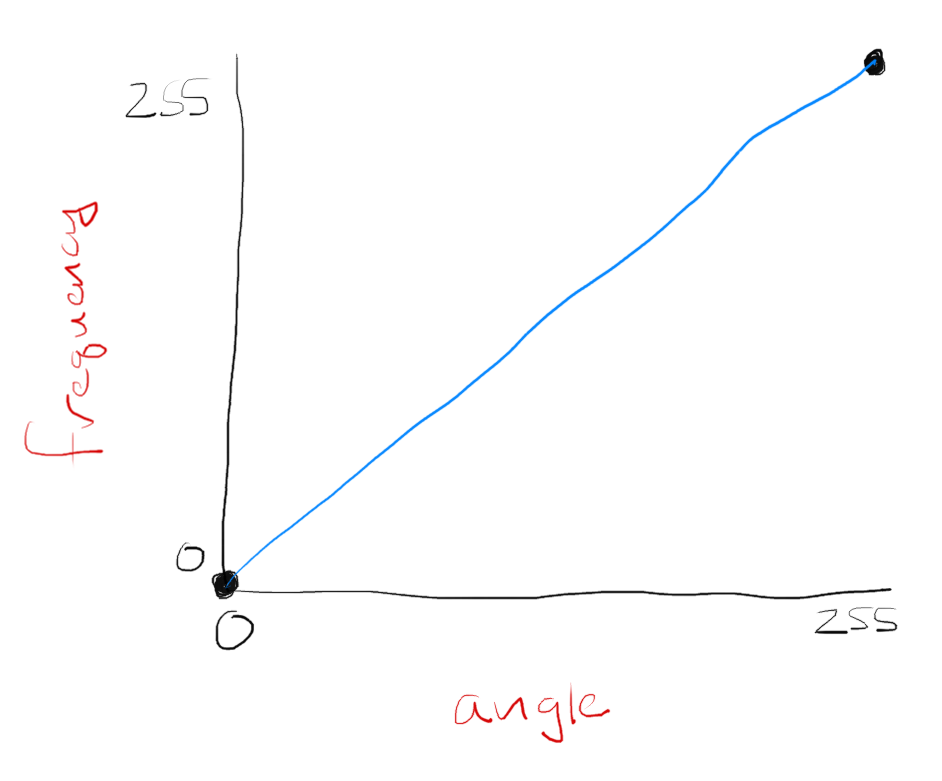What mathematical function describes this relationship between angle and frequency?We must tweak this function in two ways to achieve a better range. First, we want to push the frequencies up the y-axis away from the inaudible 0.
How do you push a function up the y-axis?Second, we want to expand the range beyond a mere 255 values.
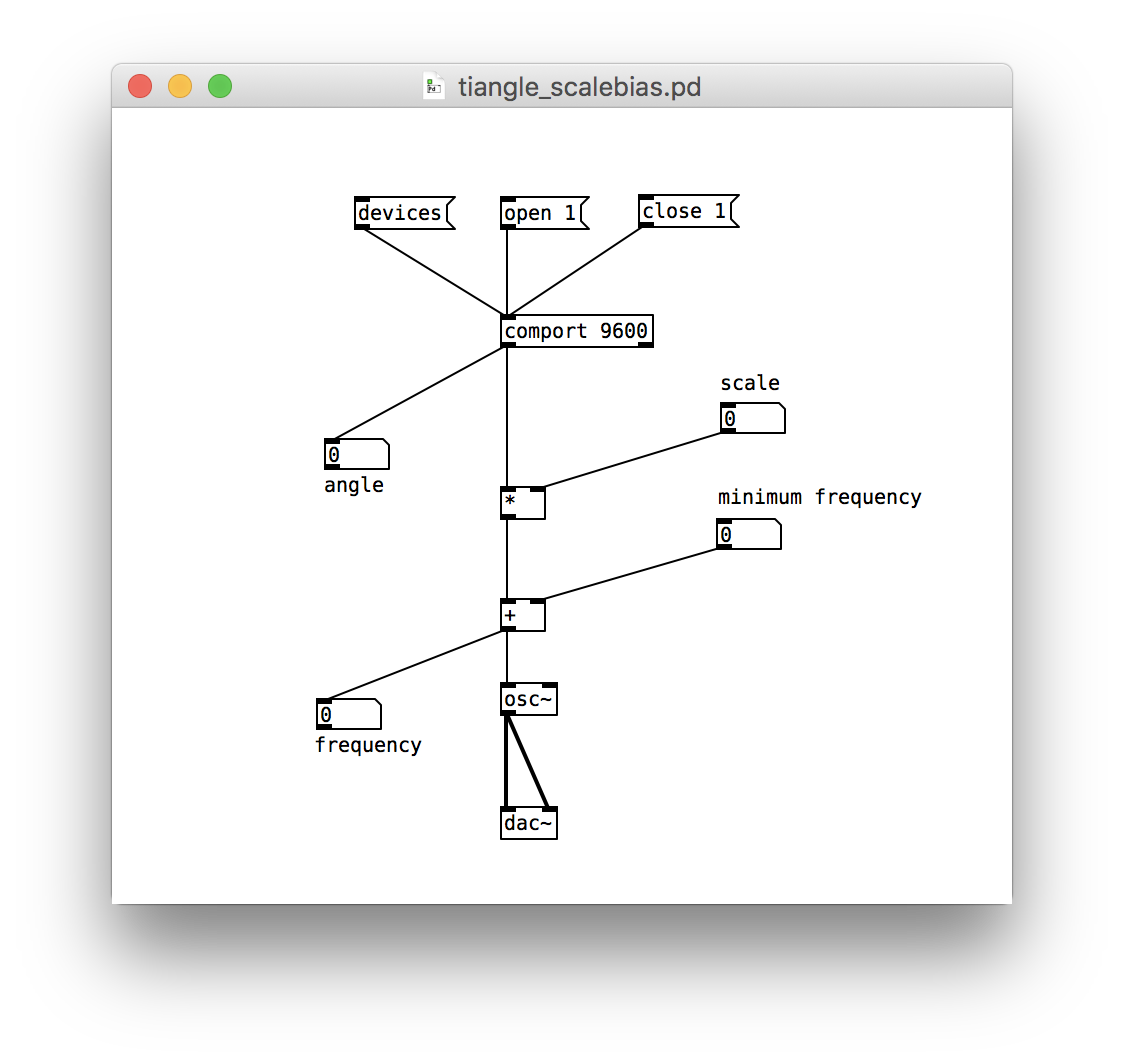
How do we widen the range of the function?We model our expanded function in Pure Data in this way:
See how the 0-255 reading leaves comport and goes through a gauntlet of arithmetic? First it gets scaled and then it gets offset.
Adjust your patch to reflect these changes. Then leave Edit Mode and test things out. Click and drag on the scale and minimum offset widgets in the patch to alter the function that maps the potentiometer’s angle to the emitted frequency.
Challenges
After you get your improved ranges working, answer the following questions on a piece of scratch paper.
- What minimum frequency and scale factor do you need to produce frequencies in the range [261, 1047]? (This range roughly goes from middle C in the fourth octave to C in the sixth octave.)
- Currently, a clockwise rotation increases the frequency. How can you adjust the parameters in Pure Data so that the potentiometer works the opposite direction? That is, when you crank it clockwise, it behaves like it was being turned counter-clockwise and spans the range [1047, 261]?