Timbre and Harmonics
This post is part of a series of notes and exercises for a summer camp on making musical instruments with Arduino and Pure Data.
Earlier we said that sounds are generated by oscillating sine or cosine waves. That was a lie. None of our musical instruments produce pure waves of a single frequency. Rather, they produce a family of waves. For instance, if I play an A in the 4th octave on my trombone, I will broadcast a wave at 440 Hz, another at 880 Hz, another at 1320 Hz, and so on.
Where did that 880 come from? And the 1320?What gives each instrument its unique sound—or timbre (rhymes with amber)—are the relative strengths of the fundamental and harmonic waves. For example, 50% of the sound’s energy might go to the fundamental frequency, 30% to the the third harmonic, and 20% to the fifth.
In this exercise, we’ll create a Pure Data patch that lets the musician control the relative strengths of the fundamental and harmonic waves.
Five-key Keyboard
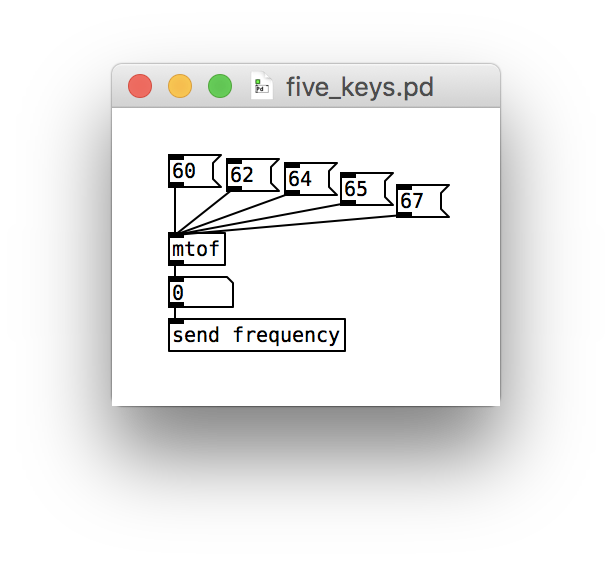
We start our patch with a little keyboard. Since we will be shaping the sound waves ourselves, we can’t use MIDI. We’ll be configuring our own oscillators all within Pure Data. However, let’s use MIDI numbers to choose what notes we want to play. We can turn a MIDI number into a frequency using the mtof (MIDI to frequency) object.
Here’s a little keyboard that provides a major pentascale starting at middle C:
For the time being, we just send the frequency along. Later we’ll add some receivers.
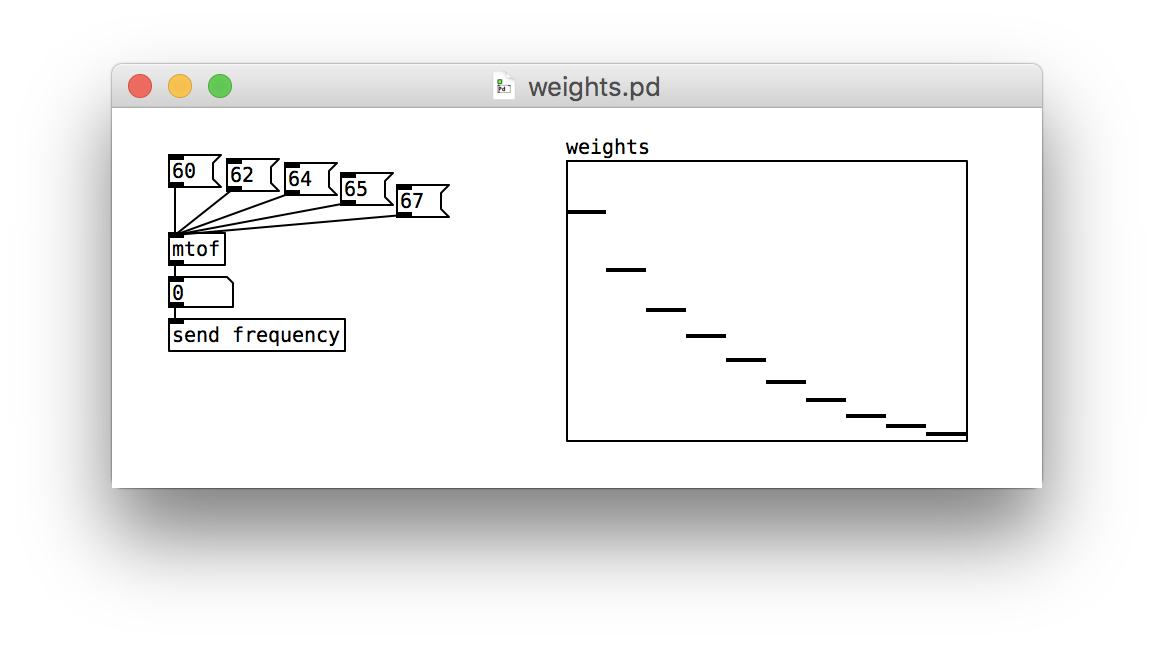
Weights
Our next step is to provide an interface for controlling the weights of the waves. We could use Pure Data’s slider objects, but since we have a collection of waves, it’s easier to use an array. Add one, name it weights, and give it a size of 10. We’ll combine 10 waves to produce our custom timbre.
After the array has been made, right-click on it and select Properties. In the Canvas Properties window, change the Y-range to span from 100 at the top to 0 at the bottom. The patch should look something like this:
When you draw on the array with the mouse, you are setting the 10 weights. The leftmost weight corresponds to the strength of the fundamental frequency.
Normalizing
Imagine someone gave you a recipe for the perfect lemonade: 3 parts sugar, 2 parts water, and 1 part lemon juice. If you go to make this recipe, these numbers aren’t in and of themselves very helpful. We first need to convert them to proportions, and then we can apply the proportions to the amount of lemonade we want to make.
According to the recipe, there are 6 parts in total. 3 of the 6, or 50%, is sugar. 2/6 or 33% is water. 1/6 or 17% is lemon juice.
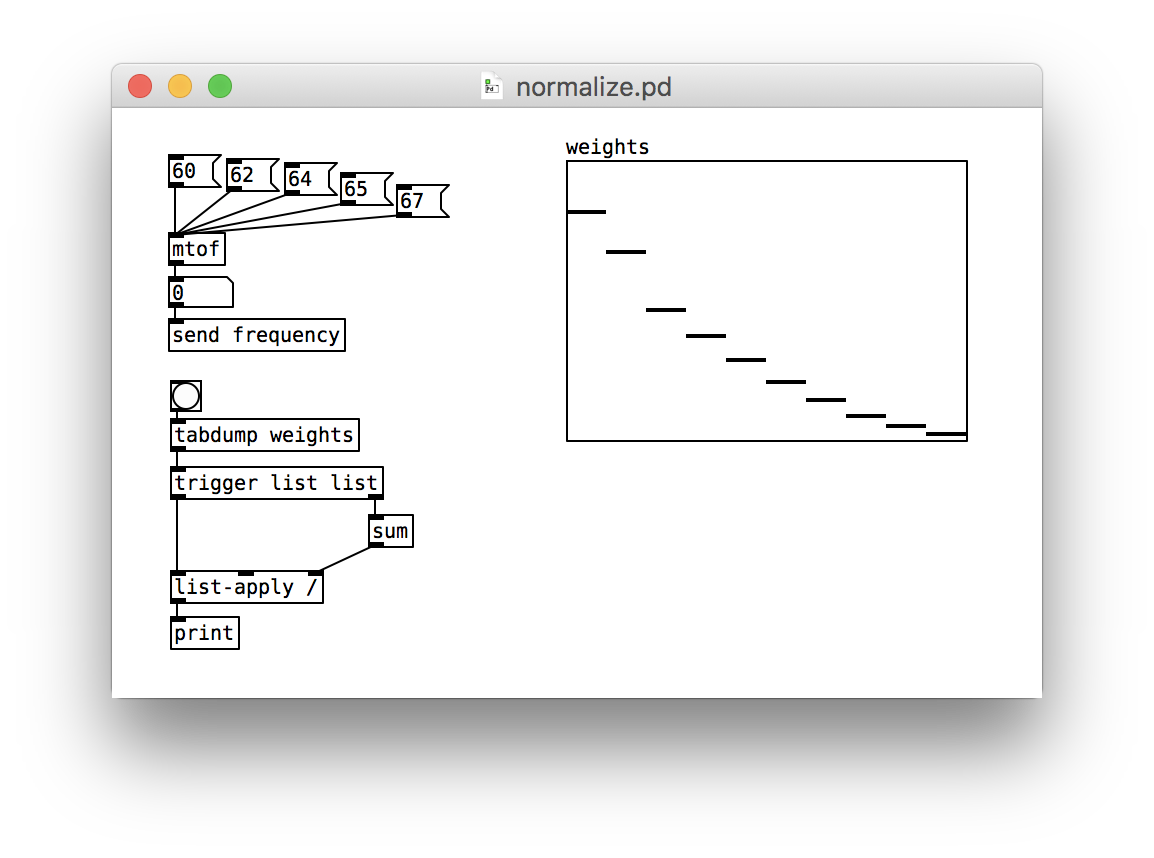
So it is with the weights in our array. They are relative weights, and we need to convert them to proportions by dividing by their total.
There are several ways we can calculate the total and divide each number. The method with the fewest steps requires a couple of packages. Click Window / Find Externals and install zexy and list-abs. You might need the extended versions of these libraries. (I’m afraid I don’t quite understand the differences between the various versions.)
We’ll use tabdump command to convert the weights array into a list. The list is then fed into a sum object to calculate the total. Then each element of the list is divided by the total using the list-apply object.
When you click on the bang, you’ll see a list of 10 numbers in the console. They should all add up to 1.
Harmonic Abstraction
With the proportions calculated, let’s now create a wave for each harmonic. Recall that harmonics are integer multiples of the fundamental frequency. We’ll say that the fundamental frequency is harmonic 1, twice the fundamental frequency is harmonic 2, thrice is harmonic 3, and so on.
Each harmonic needs its own oscillator. It will need to oscillate at the specified multiple of the fundamental frequency, and its strength will be determined by multiplying by the weight. The stronger the weight, the louder the sound. Since all the harmonics behave similarly, and there are ten of them, we should probably make an abstraction.
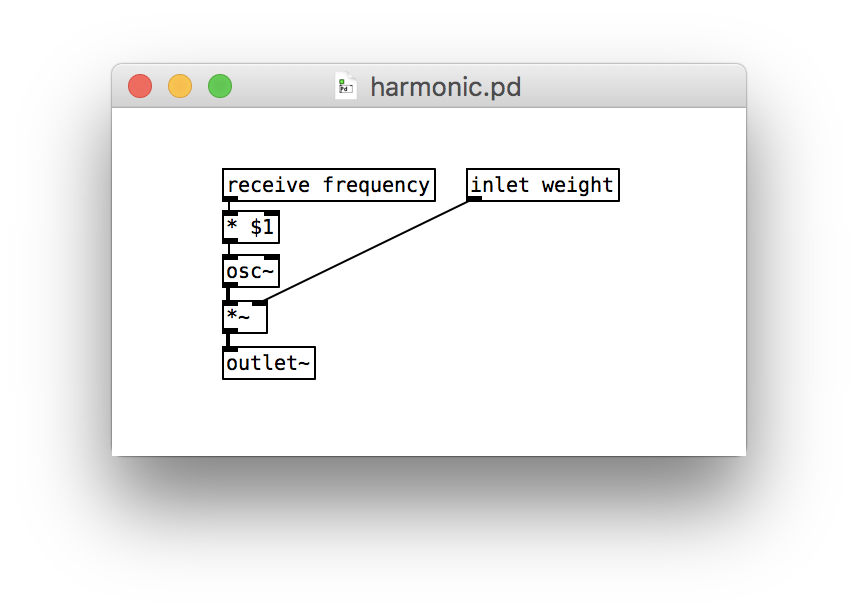
The abstraction must receive three pieces of data. The fundamental frequency will come in from the main patch through a receive. The integer coefficient will come in as a creation argument. And the weight will come in through an inlet.
We multiply the fundamental frequency by the coefficient to get the harmonic’s frequency. Then we fire up an oscillator, but scale its amplitude by the weight.
All told, our abstraction looks like this:
Combining Harmonics
The last step is to wire 10 instances of harmonic into our main patch. We pass along the integer coefficients as creation arguments. We must also pass the weights in via their inlets. The weights are locked up in a list, but we can decompose the list into 10 separate numbers using the unpack object. We write unpack f f f f f f f f f f to unpack the list into 10 floats. To add up all of the waves, we feed all the harmonics into the left inlet of a +~ object.
The end result is quite messy:
To play your new instrument, with its customizable timbre, click on the five MIDI notes. Change the timbre by drawing on the array and firing the bang. As a challenge, investigate the harmonic spectrum of the clarinet and try to emulate its sound.