Circle
This post is part of a course on geometric modeling at the Summer Liberal Arts Institute for Computer Science held at Carleton College in 2021.
Here’s your next exercise. Add a shape generator function for this shape and render it:

How would you do it?
Perhaps this seems impossible. Earlier I said that all shapes can be decomposed into triangles. That wasn’t a lie. Circles in computer graphics are just regular polygons with a large number of vertices. One way to model them is as a pizza, with a vertex in the center at which all of the very thin slices converge.
To make a pizza with six slices, we’d need to find the xy-coordinates for the vertex at 0 degrees, 60 degrees, 120 degrees, 180 degrees, 240 degrees, and 300 degrees. We also need the center, which we’ll assume is (0, 0, 0). The vertices are marked on this hex pizza:
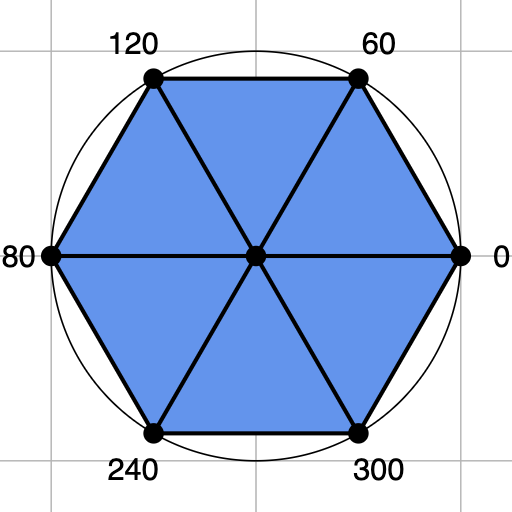
But the angles of the vertices aren’t directly useful. What we really want are the xy-coordinates of the vertices. If we had those, our positions array might look something like this:
function generateCircle(radius) {
const positions = [
xAt0, yAt0, 0,
xAt60, yAt60, 0,
xAt120, yAt120, 0,
xAt180, yAt180, 0,
xAt240, yAt240, 0,
xAt300, yAt300, 0,
0, 0, 0,
];
}
How do we find the xy-coordinates for a given angle? Suppose that the point is on the unit circle and forms an angle $A$ with the x-axis. Well, for angles that are less than 90 degrees, the vertex forms a right triangle that looks like this:

Using our trigonometric knowledge, we relate the sides of the triangle:
We solve for the xy-coordinates:
Our illustration only tells us how to find the xy-coordinates when the angle is less than 90 degrees. These same equations do happen to hold for larger angles. We won’t prove that.
Equipped with this knowledge, we update our code:
function generateCircle(radius) {
const positions = [
radius * Math.cos( 0), radius * Math.sin( 0), 0,
radius * Math.cos( 60), radius * Math.sin( 60), 0,
radius * Math.cos(120), radius * Math.sin(120), 0,
radius * Math.cos(180), radius * Math.sin(180), 0,
radius * Math.cos(240), radius * Math.sin(240), 0,
radius * Math.cos(300), radius * Math.sin(300), 0,
0, 0, 0,
];
}
Oh, wait. JavaScript expects radians, not degrees. We convert:
function generateCircle(radius) {
const positions = [
radius * Math.cos( 0 * Math.PI / 180), radius * Math.sin( 0 * Math.PI / 180), 0,
radius * Math.cos( 60 * Math.PI / 180), radius * Math.sin( 60 * Math.PI / 180), 0,
radius * Math.cos(120 * Math.PI / 180), radius * Math.sin(120 * Math.PI / 180), 0,
radius * Math.cos(180 * Math.PI / 180), radius * Math.sin(180 * Math.PI / 180), 0,
radius * Math.cos(240 * Math.PI / 180), radius * Math.sin(240 * Math.PI / 180), 0,
radius * Math.cos(300 * Math.PI / 180), radius * Math.sin(300 * Math.PI / 180), 0,
0, 0, 0,
];
}
This code is noisy and a bit more repetitive, but we’ll fix that eventually. What would change if we only wanted five slices? Seven? Eight? For a pizza with $n$ slices, the angle of each slice is:
Instead of hardcoding a fixed number of vertex positions, we add them in a loop. The number of vertices comes in as a parameter. That leads to this code:
function generateCircle(radius, n) {
const radiansPerWedge = 2 * Math.PI / n;
const positions = [];
for (let i = 0; i < n; i += 1) {
const radians = radiansPerWedge * i;
positions.push(radius * Math.cos(radians), radius * Math.sin(radians), 0);
}
positions.push(0, 0, 0);
}
That covers the list of positions. We also need the list of triangles. All triangles will include the center position, which is at index $n$ in the positions array. Each will also include a vertex from the outer perimeter and its successor. The successor of the final perimeter vertex perimeter is the first vertex, which is at index 0. We compute the successor with wrapped addition. This algorithm translates into the following code:
function generateCircle(radians, n) {
// calculate positions as above
const triangles = [];
for (let i = 0; i < n; i += 1) {
const iNext = (i + 1) % n;
triangles.push(i, iNext, n);
}
return {positions, triangles};
}
And there we have our circle generator. It also generates hexagons, heptagons, nonagons, squares, equilateral triangles, and all the regular polygons. Try rendering it with various values for the radius and number of wedges.