CS 430: Lecture 2 – Syntax
Dear students,
Today we look at the first steps of how a program becomes an executable. The source code that we write is a foreign language to the computer. It must be translated into a language that the machine does know. That’s the job of the compiler or interpreter. Translation is a process with multiple stages. Only two of these stages concern us at this point in the course: lexing and parsing.
Both of these stages deal with the syntax of a language. By syntax, we mean the structure or form of expressions in a language. In these stages we are not at all concerned with semantics—the meaning—of the language. Consider the expression i++. Syntactically, this expression is an identifier i followed by operator ++. Semantically, this expression evaluates to the original, unincremented value bound to the name i and has a side effect on incrementing i. Today we focus on syntax and ignore semantics.
Lexing
Lexing is the task of grouping the individual characters into coherent chunks. These chunks are called tokens or lexemes. You are familiar with many tokens: public, main, ;, ++, return, 3.14159, and so on.
To recognize a particular kind of token, we build a little machine. Rather than code this machine, we’ll just think about how it works using a diagram. For example, here’s a machine for recognizing integer literals:
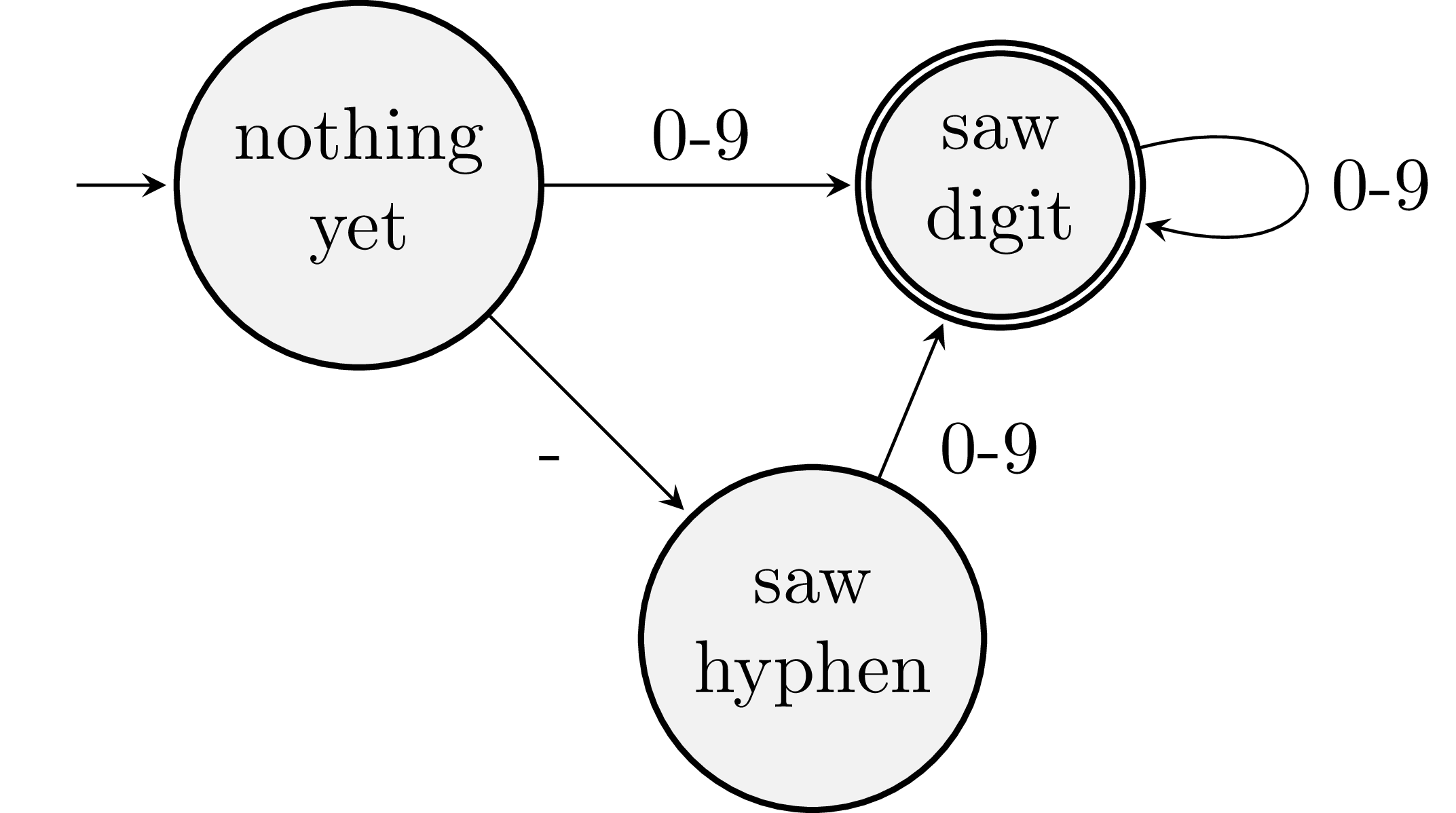
In the nothing yet state, which is where we start, we haven’t read any of the characters in the source code. If we see a digit, we move to the saw digit state. If we see more digits, we stay in that state. Alternatively, suppose we see a hyphen first. Then we’d go into the saw hyphen state. If we then see a digit, we’d find ourselves in the saw digit state.
When we encounter a character that isn’t legal for our current state, we stop reading. If the state is an accepting state, then we’ve found ourselves a legal token. Accepting states are marked with a double outline. If we’re not in an accepting state, then we have bad source code and we issue an error. For example, if the source is -a, we read the -, land in saw hyphen, and cannot transition on a. We’re not in an accepting state, so we reject this text as it’s not an integer literal. On the other hand, if the source is 8675309 * 2, we read the digits 8675309, land in saw digits, and cannot transition on the space. We’re in an accepting state, so we record the token and then try lexing another token using the remaining input * 2.
What would a machine for recognizing identifiers look like? In many languages, identifiers must start with a letter or an underscore. Subsequent symbols can be letters, numbers, or underscores.
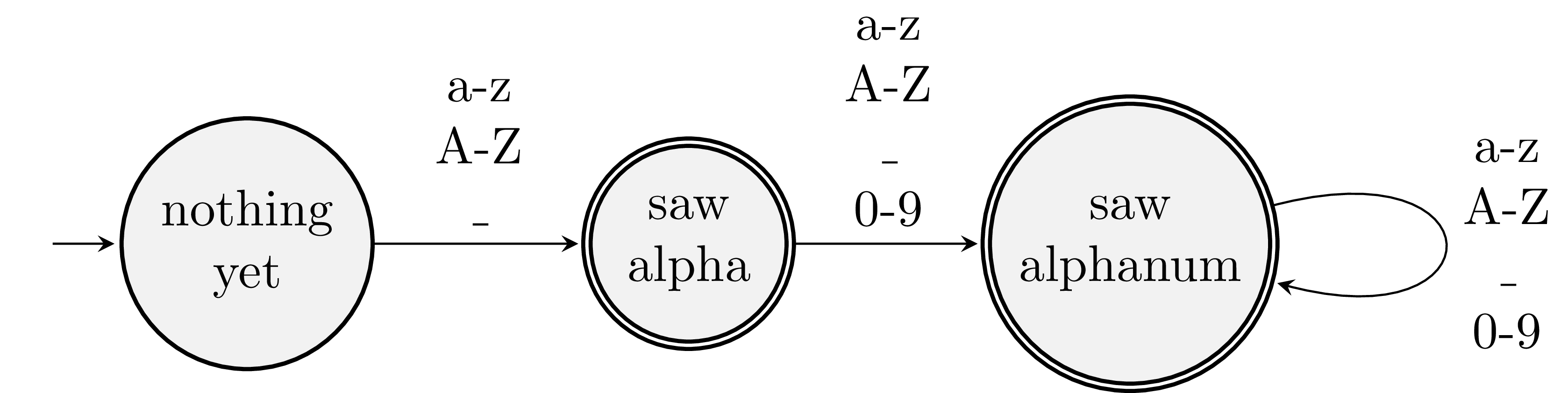
Single-letter identifiers like i will drop us off in saw alpha. These are valid identifiers, so we make this an accepting state. It’s legal to have more than one. There’s a rule in lexing that the machine matches as much of the input that it can. The source ii++ will yield a single identifier token for ii rather than two for i and i. Same with ++.
What would a machine for recognizing string literals look like? We only accept strings that have both opening and closing quotation marks. Nearly any character can appear between them. Another quotation mark is not possible unless we escape it. We add an extra state to our machine to handle escaped characters.
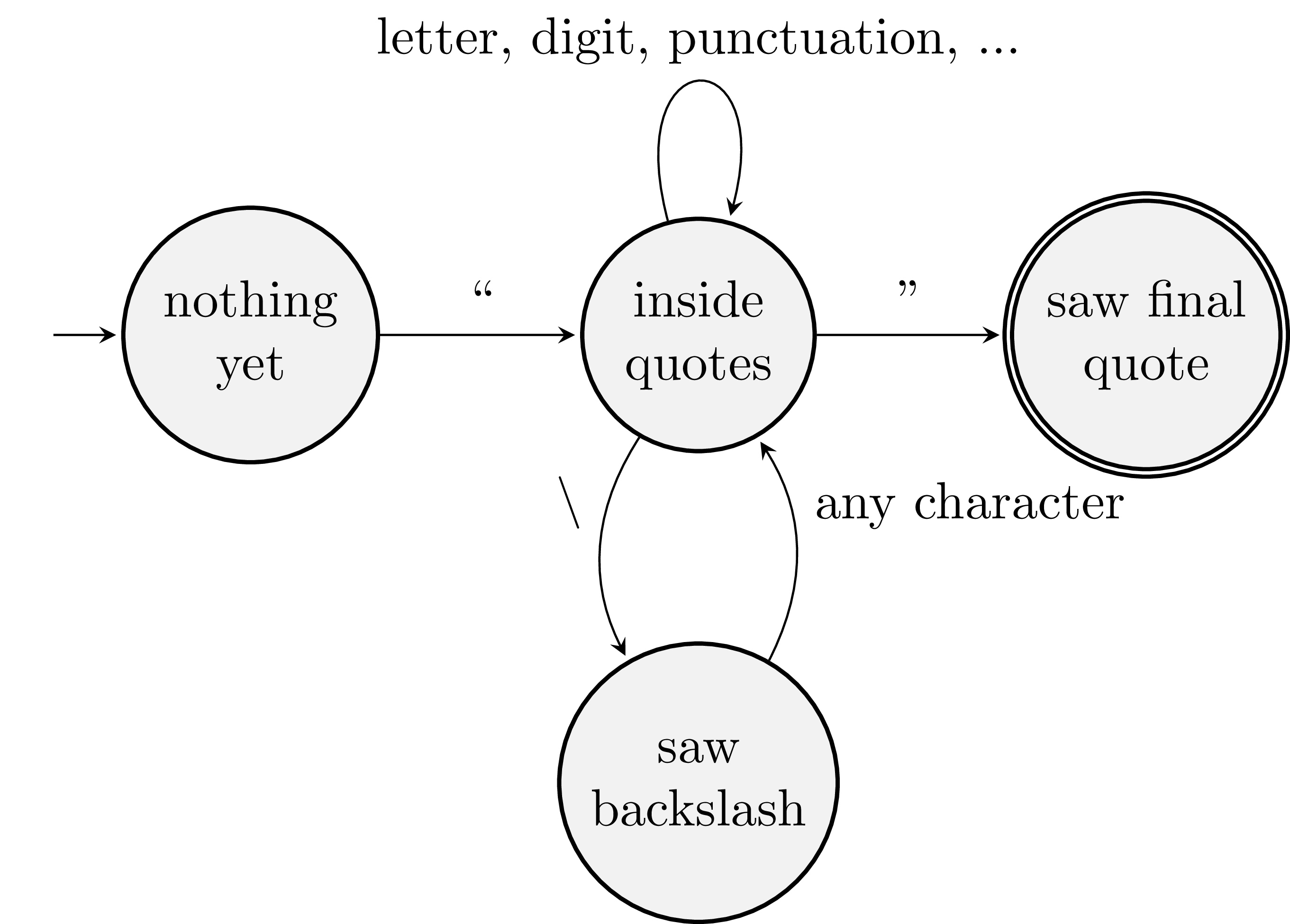
To build a complete lexer, we construct state machines for all the different kinds of tokens in our language and then mesh them together. One way to implement a lexer is with a loop and a bunch of conditional statements. The end result is an array of tokens. Each token generally has three properties:
- token type (e.g., identifier, integer literal, semi-colon, right parenthesis, …)
- source text (sometimes the text is implied by the token type, but not always, as is the case for identifiers)
- location
This list of tokens is passed along to the next stage of translation: parsing.
Parsing
When you read a book, you take in a sequence of tokens. To make sense of the sequence, you parse the words and punctuation according to the grammar of the language. You figure out the subject, the verb, and direct and indirect objects. So too must the compiler or interpreter parse the tokens from the lexing phase. It does this by fitting the tokens to the grammar of the programming language.
To explore the notion of a grammar, let’s work with an imaginary language where you can store, add, and print integers. Here’s an example program:
a = 10 puts a puts a + 1 a = a + 1 b = a puts a + b
We express the grammatical rules of this language using a notation called Extended Backus-Naur Form (EBNF). A program is 0 or more statements, which leads us to this rule:
program -> statement* EOF
A statement can either be a puts statement or an assignment, which leads us to this rule:
statement -> identifier = expression
| puts expression
An expression can either be an integer literal, a variable name, or an addition, which leads us to this rule:
expression -> integer
| identifier
| expression + expression
These expansion rules are called productions. There are six of them in this grammar. Some of the symbols indicate what kind of token is expected. Other symbols indicate that another production needs to be applied. These latter are the grammar’s non-terminals, while the symbols standing in for tokens represent the terminals. Every grammar has a special starting non-terminal, which is usually listed first. In this case, that symbol is program.
There are various algorithms for implementing a parser. The most intuitive way is to write a function for each non-terminal, with if statements to choose which productions to apply and loops to repeat. In pseudocode, that might look something like this:
def program()
statements = []
while token isn't EOF
s = statement()
append s to statements
return new Program(statements)
def statement()
if current token is identifier
id token = current token
assert equals token
e = expression()
return new Assignment(id token, e)
else if token is puts
e = expression()
return new Puts(e)
def expression()
if current token is integer
return new Integer(current token)
else if current token is identifier
return new Variable(current token)
else
a = expression()
assert plus token
b = expression()
return new Add(a, b)
This method of parsing is called recursive descent. It’s a human-friendly algorithm. There are a number of tools that will take in your grammar and automatically generate a parser. The algorithms they use tend to be more complex than recursive descent, and we won’t examine them. If translating source code seems interesting to you, consider taking CS 432.
Derivations
There are several kinds of grammar-related ideas that you are expected to know as a computer scientist. The first is how to derive an utterance or sentence from its grammar. Suppose you have the string xoxox and this grammar:
S -> x Z Z -> o x Z | o x
A derivation is a sequence of expansions that goes from the starting symbol to the string, applying one production at a time until only terminals remain, like this:
S -> x Z -> x o x Z -> x o x o x
As grammars get more complex, we see that sometimes we have decisions to make when deriving. Consider this grammar for composing boolean expressions out of boolean literals and the binary logical operators:
P -> P || Q | Q Q -> Q && B | B B -> true | false
Here’s one way we might derive the expression true && false || true:
P -> P || Q -> Q || Q -> Q && B || Q -> B && B || Q -> true && B || Q -> true && false || Q -> true && false || true
Notice how we only expand the leftmost non-terminal at each step? When we stick to this pattern, we end up with a leftmost derivation. This is the kind of derivation that we see in a recursive descent parser. Other kinds of parsers expand the rightmost non-terminal, producing a rightmost derivation, which would look like this for our expression:
P -> P || Q -> P || true -> Q || true -> Q && B || true -> Q && false || true -> B && false || true -> true && false || true
Parse Trees
In addition to derivations, you will encounter tree representations of how an utterance is parsed. The root of the tree is the starting symbol. Its children are the terms of the production that is applied. Any non-terminals have children of their own. The terminals are leaf nodes.
For the expression true && false || true, we have the following parse tree:
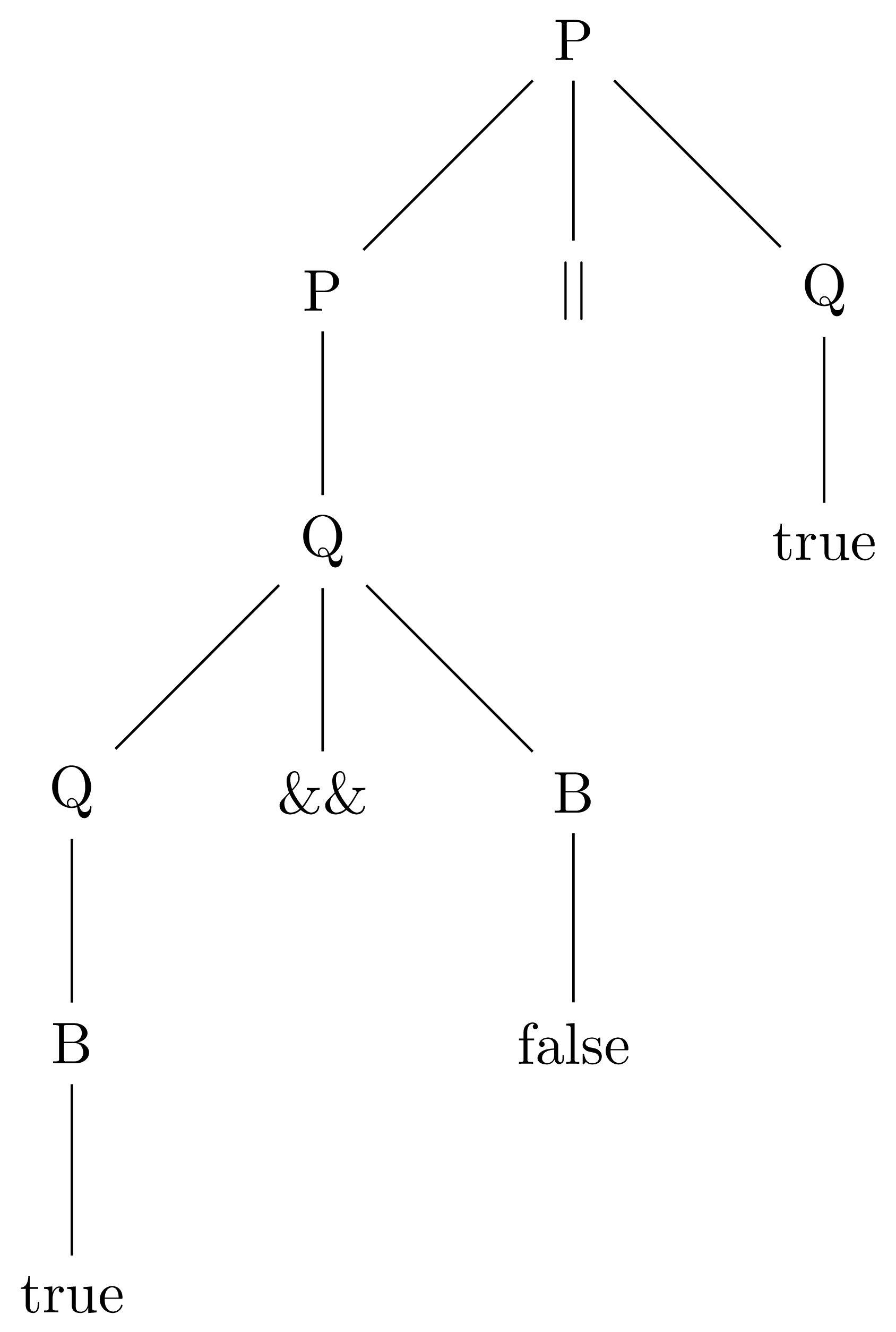
There are not leftmost or rightmost versions of parse trees. The same tree effectively shows all non-terminals at a particular level of depth expanded in parallel.
Precedence
A nice feature of parse trees is that they make clear the precedence of the operators. The operators that appear lower in the tree have higher precedence. In our example expression, && is lower and therefore has higher precedence.
The lower-higher comparison is only valid as a precedence check if the operators do not have the same distance from the start symbol in the grammar. If the operators do have the same distance, they have equal precedence. For example, suppose we have the following grammar:
S -> S + T | S - T | T T -> integer
The + and - operators have the same precedence because they are both one production away from S.
Associativity
If + and - have the same precedence, how then do we know which one gets evaluated first? Let’s examine the leftmost derivation of 5 - 2 + 1:
S -> S + T -> S - T + T -> T - T + T -> 5 - T + T -> 5 - 2 + T -> 5 - 2 + 1
We have this corresponding parse tree:
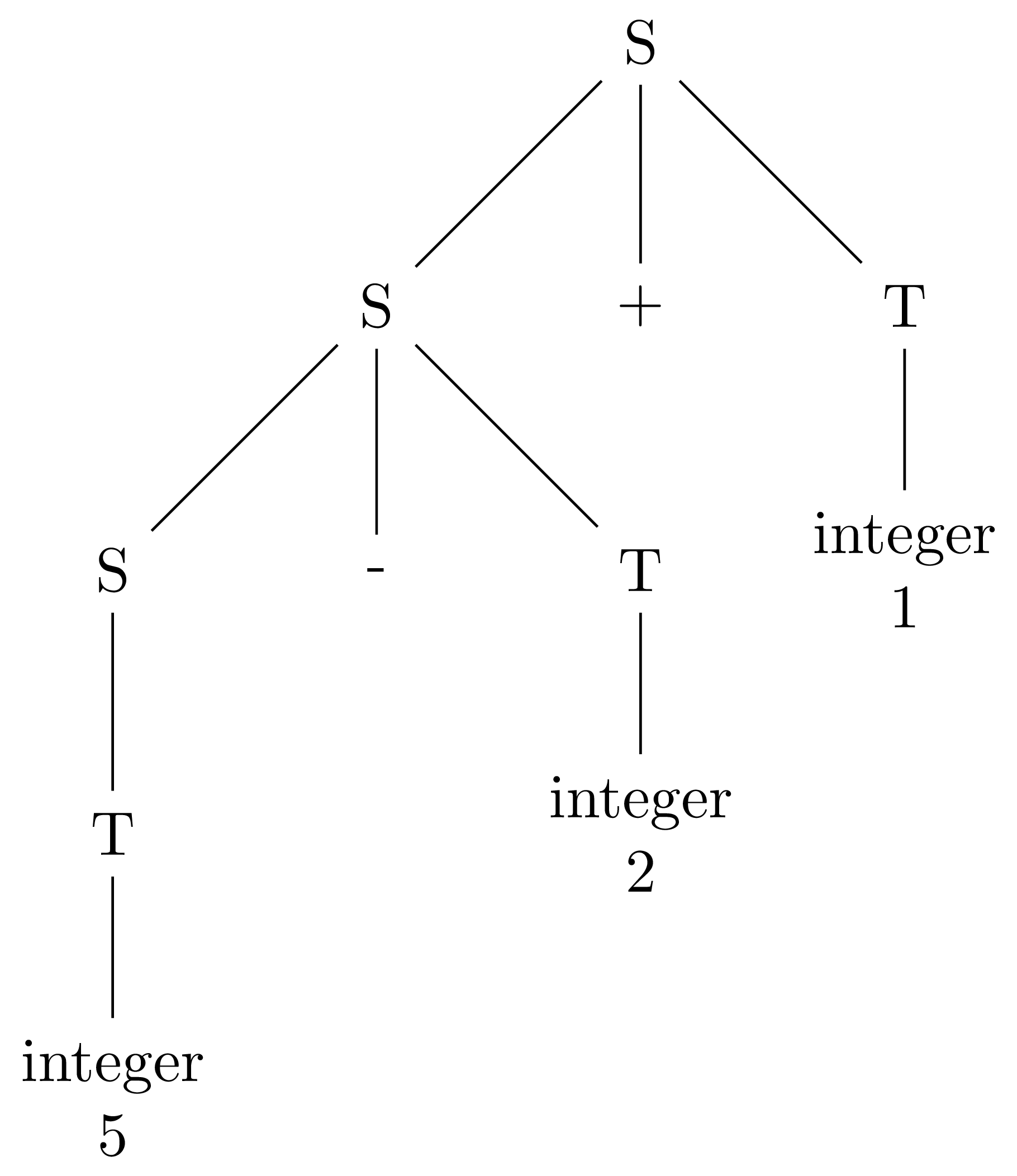
The rules of the operators’ associativity are baked into the grammar. Subexpressions are forced by this grammar to appear in the left operand, which means that these operators are left associative. Left associative operations are evaluated from left to right.
Let’s see another example with our boolean expression grammar. Suppose we have the expression false || false || false. We have this leftmost derivation:
P -> P || Q -> P || Q || Q -> Q || Q || Q -> B || Q || Q -> false || Q || Q -> false || B || Q -> false || false || Q -> false || false || B -> false || false || false
Is the || operation left associative or right associative? It’s left associative. This grammar, just like the last one, pushes nested operations down in the left child.
Do you know any operations that are right associative—that are evaluated from right to left? Many of the unary operators are, as evidenced by !!true. The binary and exponentiation operators tend to be right associative.
Let’s add productions to our arithmetic grammar to support a right-associative exponentiation operator. This was our original grammar:
S -> S + T | S - T | T T -> integer
Exponentiation has higher precedence, so we want to force it to be lower in the parse tree than + and -. We also want to force nested exponentiations to be in the right child in order to make it right associative. Both of these wants are satisified by this new grammar:
S -> S + T | S - T | T T -> U ^ T | U U -> integer
Ambiguity
Grammars are neat. They unite the language instincts inside of us with the precision and formality needed for translating source code. But not just any grammar is acceptable. We must avoid ambiguity.
An ambiguous grammar is one that allows us to derive the same utterance more than one way. Have a look at this grammar:
A -> V = E E -> E # E | V V -> a | x | y | z
Let’s start deriving a = x # y # z using a parse tree:
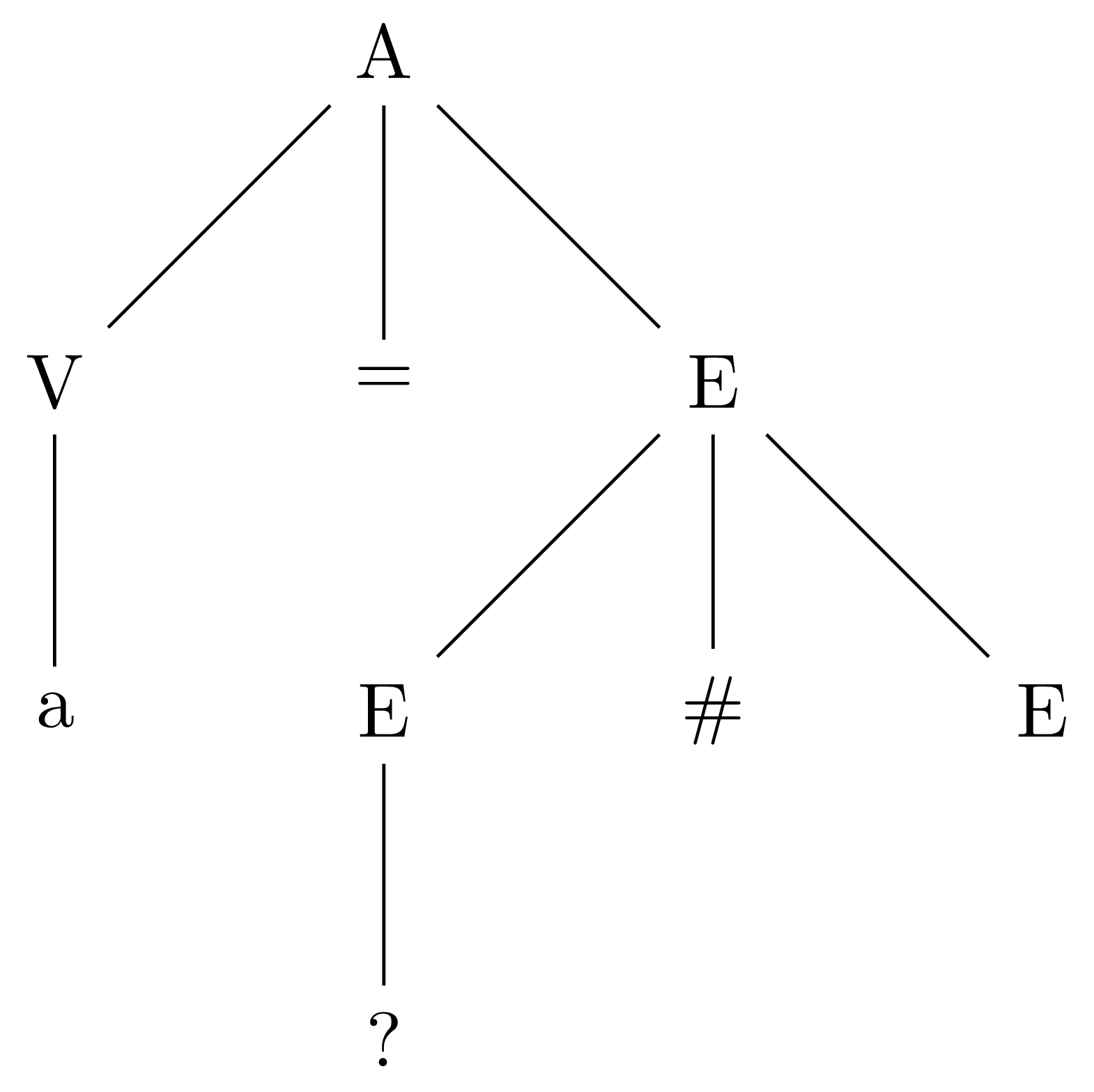
When we go to expand the first E in E # E, we find that we have a choice. We can use either the E # E production or the V production. If we apply E # E, we arrive at this tree:
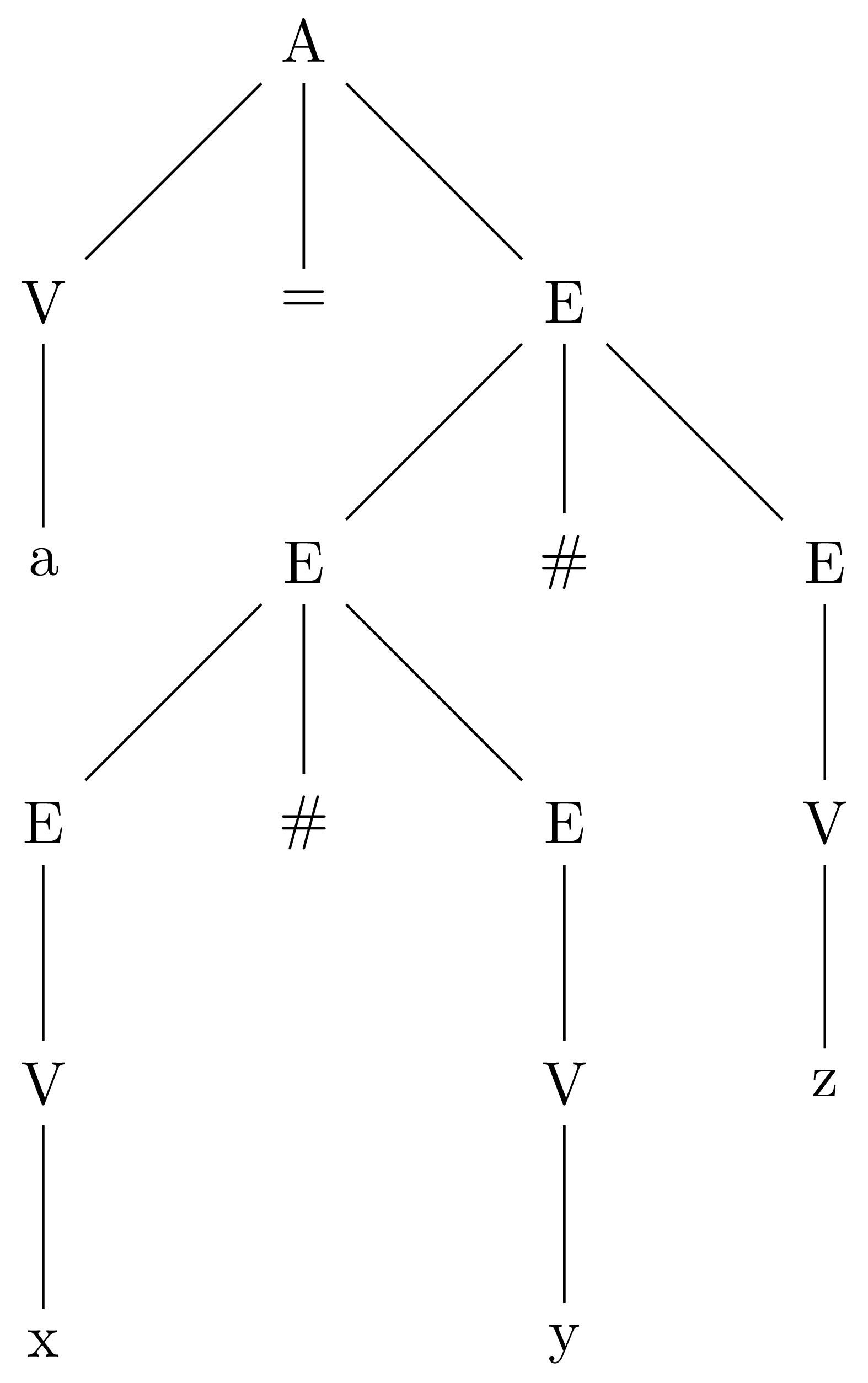
If we apply V, we arrive at this tree:
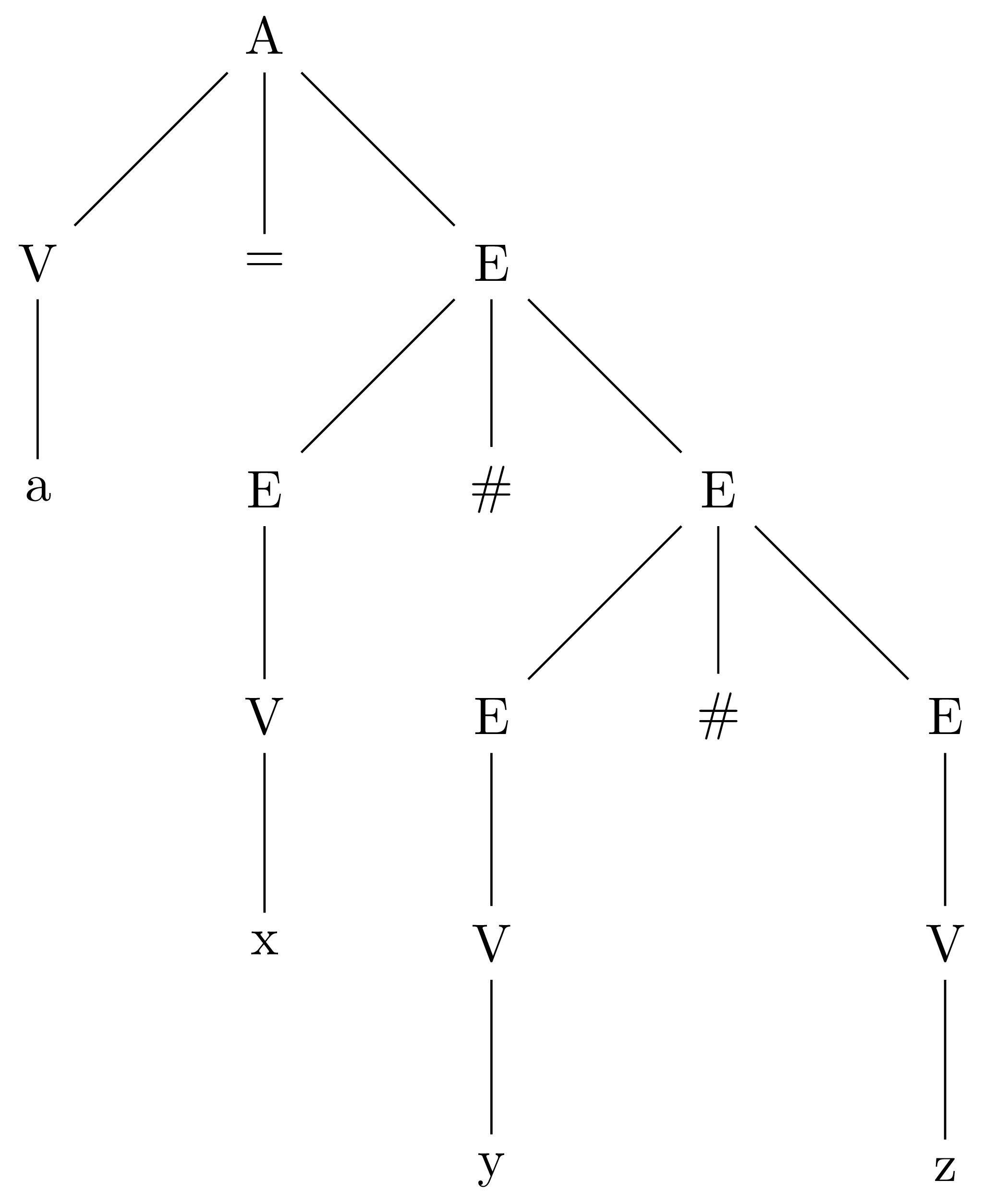
Ambiguity is a bad feature to have in a grammar. We don’t want different compiler implementations producing different programs from the same source code. We’d remove this particular ambiguity by fixing the associativity of the # operator. To make it left associative, we’d use this grammar:
A -> V = E E -> E # V | V V -> a | x | y | z
Conclusion
The notion of a grammar lies behind every programming language that we use. The grammar enforces the operator precedence and associativity. The grammar informs the design of the parser. The grammar impacts the quality of error messages.
If you want to write a programming language, the best place to start is by writing the grammar. The rest of your work falls out from there.
Even if you don’t want to write your own language, understanding the role of grammars will make writing code in existing languages feel less like a game of chance. You don’t need to appeal to a higher power to get your code to compile. You just need to follow the grammar.
Grammars also help explain some of the syntactic choices that language designers make. Those semi-colons and curly braces, for example, make writing the parser easier.

P.S. It’s time for a haiku!
First we kill a tree
We draw what on the paper?
Dead, upside-down trees